Sizden gelen soru:
Katı cisimlerin alanları prizmalar ve piramitlerin?
Cevap:
Prizmaların özellikleri, prizmaların çeşitleri, prizmaların formüller, prizmaların alanları ve prizmaların hacimleri hakkında detaylı bilgileri;
Piramitlerin özellikleri, piramitlerin çeşitleri, piramitlerin formüller, piramitlerin alanları ve piramitlerin hacimleri hakkında detaylı bilgileri;
aşağıda detaylı bir şekilde vermeye çalıştık.Umarız faydalı olur.
Prizmaların Özellikleri ve Formülleri
Tabanları birbirine eş herhangi bir çokgen ve yan yüzeyleri taban düzlemlerine dik birer dikdörtgen olan cisimlere dik prizmalar denir. Prizmalar taban şekillerine göre adlandırılırlar. Örneğin kare dik prizma, üçgen dik prizma gibi.
Dik Prizmanın Özellikleri
1) Alt ve üst tabanları eş ve paraleldir.
2) Yan yüzeyleri dikdörtgenlerden oluşmuştur.
3) Yan ayrıtları aynı zamanda dik prizmaların yüksekliğidir.
4) Bir dik prizmanın yanal alanı, taban çevresi ile yüksekliğin çarpımına eşittir.
5) Bir dik prizmanın tüm alanı, yanal alanı ile iki taban alanının toplamına eşittir.
6) Bir dik prizmanın hacmi, taban alanı ile yüksekliğin çarpımına eşittir.
7) Bir dik prizmanın; köşe sayısı K, yüz sayısı Y, ayrıt sayısı A ile gösterilirse bunlar arasında K+Y-A=Z bağıntısı vardır.
A) Kare Dik Prizma
Tabanı kare olan dik prizmaya kare dik prizma denir. Kare prizmanın alt ve üst tabanları birbirine eş iki kare, yan yüzeyleri ise birbirine eş dikdörtgenlerdir.
Taban Çevresi = 4a, Taban Alanı = a2 , Yanal Alanı = 4 ah
Bütün Alanı : A = 2 Ta + Ya
= 2a2 + 4 ah = 2a (a+2h)
Hacim = a2 .h Cismin köşegeninin uzunluğu : k =
B) KÜP
Bütün yüzleri karesel bölge olan dik prizmaya küp denir.
Taban Çevresi = 4a, Taban Alanı = a2 , Yanal Alan = 4a2
Bütün Alan = 2 Ta + Ya Hacmi = a3, Yüzey Köşegeni = a
= 2 a2 + 4 a2 = 6 a2 Cisim Köşegeni = a
C) DİKDÖRTGENLER PRİZMASI
Bütün yüzeyleri dikdörtgen olan dik prizmaya dikdörtgenler prizması denir.
Taban Çevresi = 2.(a+b), Taban Alanı = a.b
Yanal Alanı = 2.(a+b).c, Bütün Alan = 2.(ab+ac+bc)
Hacmi = a.b.c., Cisim Köşegeni =
D) ÜÇGEN DİK PRİZMA
Tabanı üçgen olan dik prizmaya, üçgen dik prizma denir.
Sayfa 226 üçgen prizma ekle.
Tabanları üçgen ve bu üçgenler birbirine eştir.
Yan yüzeyleri dikdörtgendir.
Yanal ayrıtlar eş ve birbirine paraleldir.
Taban çevresi = a+b+c, Taban alanı = (a+b+c).h
Bütün alanı = 2.Ta+Ya, Hacmi = Ta x h
E) DÜZGÜN ALTIGEN DİK PRİZMA
Tabanı altıgen olan dik prizmaya, düzgün altıgen dik prizma denir.
Yan yüzeyleri birbirine eş 6 dikdörtgenden oluşur.
Tabanlarındaki altıgen 6 eş kenar üçgeninin birleşmesinden oluşur.
Taban alanı = 6 . Yanal alan = 6.a.h
Bütün alan = 2.Ta + Ya, Hacmi = Ta . h
= 2.3 ak + 6 ah = 3 ak . h
= 6 a.(k + h)
Piramitlerin Özellikleri ve Formülleri
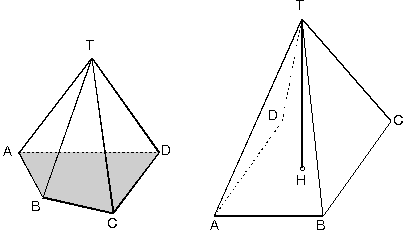
Bir düzlemde kapalı bir bölge ile bu düzlemin dışında bir T noktası alalım. Kapalı bölgenin tüm noktalarının T noktası ile birleştirilmesi sonucunda oluşan cisme piramit denir.
Eğer piramidin tabanı düzgün çokgense bu tip piramitlere düzgün piramit denir.T noktası piramidin tepe noktasıdır. Kapalı bölge ise piramidin tabanıdır. Piramit; tabanı oluşturan şeklin ismiyle adlandırılır. Taban kare ise, kare piramit; taban altıgense altıgen piramit gibi.
T noktasının taban düzlemi üzerindeki dik izdüşümüne H dersek [TH] piramidin yüksekliği olur.
|TH| = h biçiminde yazılır. [TA], [TB], [TC]… piramidin yanal ayrıtlarıdır.
Piramitlerin hacmi taban alanı ile yüksekliğin çarpımının üçte biri kadardır.
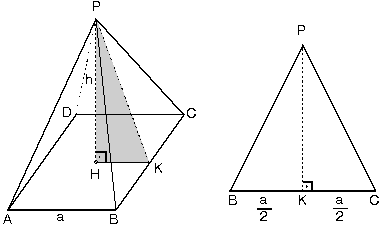
1.Kare Piramit
İkizkenar üçgenlerin taban uzunlukları piramidin tabanının bir kenarına eşittir.Kare piramidin tabanı kare biçimindedir. Yan yüzeyleri ise dört adet ikizkenar üçgenden oluşur.
|PH| = h piramidin yüksekliğidir.
Yan yüz yüksekliği |PK| dır.
Tabanının bir kenarına a dersek
|HK| = a/2 olur.
Buradan yan yüz yüksekliği
|PK|2 = h2 + (a/2 )2 olur.
Hacim = (a2.h) / 3
Tüm alan yan yüz alanları ile taban alanının toplamına eşittir.
2. Eşkenar Üçgen Piramit
Tabanı eşkenar üçgen olan piramitlere eşkenar üçgen piramit denir.
√ : Karekök simgesi
Taban Alanı (a2.√3)/4 olduğundan
Hacim = h.(1/3).((a2.√3)/3)
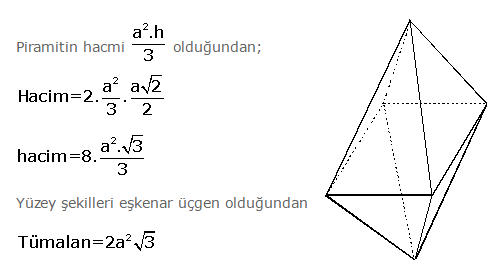
3. Düzgün Dörtyüzlü
Bir ayrıtı a olan düzgün dörtyüzlününDört yüzü de eşkenar üçgenlerden oluşan cisimdir. Yükseklik, tabanı oluşturan üçgenin ağırlık merkezine iner.
4. Düzgün Sekizyüzlü
Bütün ayrıtları birbirine eş ve yüzeyleri sekiz eşkenar
üçgenden oluşan cisme düzgün sekizyüzlü denir.
Bir ayrıtına a dersek yan yüz yüksekliği (a.√3)/2 olur.
5. Düzgün Altıgen Piramit
Tabanı düzgün altıgen olan piramide düzgün altıgen piramit denir.
Yan yüzeyleri altı adet eş ikizkenar üçgenden oluşur.
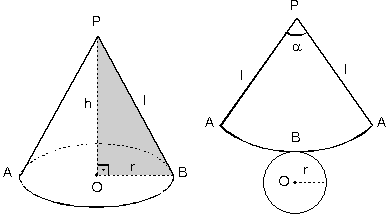
KONİ
Burada;Tabanı daire biçiminde olan piramite koni adı verilir.
Taban yarıçapı |OB| = r
Cisim yüksekliği |PO| = h olur.
|PA| = |PB| = l uzunluğuna ana doğru denir.
POB dik üçgeninde,
h2 + r2 = l2 bağıntısı vardır.
Koninin yanal alanı bir daire dilimidir.
Hacim = πr2.h . (1/3)
Daire diliminin alanı, yay uzunluğu ile yarıçapın çarpımının yarısıdır. Yay uzunluğu taban çevresine eşit olduğundan,
Yanal alan= pr2+prl
Tüm alan bulunurken, taban alanı da ilave edilir.
Tüm alan = šr2 + šrl
- Daire diliminin merkez açısına a dersek
(α/360) = r/l oranı elde ederiz
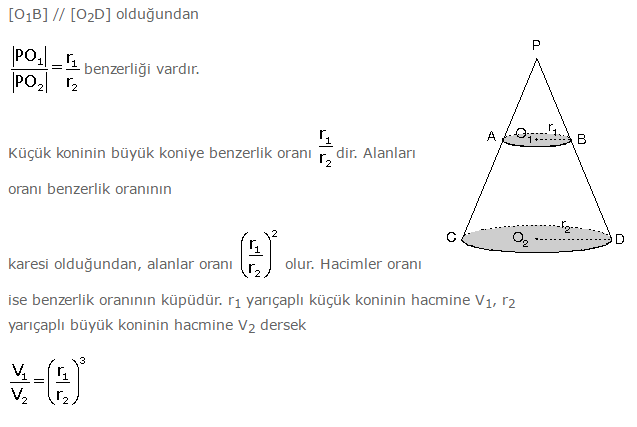
- Yükseklikleri ve taban yarıçapları eşit olan iki cismin hacimleri de birbirine eşittir.
- Üçgensel şekiller bir kenarı etrafında döndürüldüğünde koni elde edilir.şekildeki ABC dik üçgeninin AB kenarı etrafında döndürülmesi ile |BC| yarıçaplı ve yüksekliği |AB| olan koni elde edilir.
Kesik piramitlerin hacimleri bulunurken cisim piramide tamamlanır.


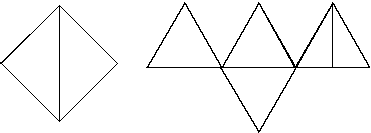

“Prizmaların ve Piramitlerin Özellikleri, Formülleri, Alanları, Hacimleri Nelerdir?” için 2 yanıt
ödevime çok yardımcı oldu
teşekkürler ödvim için lazıımdı