Birinci Grup Matematikçiler
- Thales (M.Ö. 624-547),
- Pisagor (M.Ö. 569-500),
- Zeno (M.Ö. 495-435),
- Eudexus(M.Ö. 408-355),
- Öklid (M.Ö. 330?-275?),
- Arşimed (M.Ö. 287-212),
- Apollonius (M.Ö. 260?-200?),
- Hipparc-hos (M.Ö. 160-125),
- Menaleas (doğumu, M.Ö. 80)
- İskenderiyeli Heron (? -M.S.80) ,
- Batlamyos (85- 165) ve Diophantos (325-400)
Thales
Miletli Thales (Θαλῆς ὁ Μιλήσιος, d. MÖ 624 – ö. MÖ 546), Sokrates öncesi dönemde yaşamış olan Anadolulu bir filozoftur. İlk filozoflardan olduğu için felsefenin ve bilimin öncüsü olarak adlandırılır. Eski Yunan’ın Yedi Bilge’sinden ilkidir. Ticaretle uğraşmış ve bu nedenle Mısır’da bulunmuştur. Elimize ulaşmış hiçbir metni yoktur. Yaşadığı döneme ait kaynaklarda da adına rastlanamaz ancak hakkındaki bilgiler Herodot ve Diogenes Laertios gibi antik yazarlardan edinilir. Bertrand Russell’e göre Felsefe Thales’le başlamıştır.
Diogenes Laertios’un söylediğine göre, Yedi Bilgeler Atina’da MÖ 582 civarında kuruldu. Thales Yedi Bilgelerin arasında yer almaktadır.
Astronomi
Herodot’a ve Eudemos’a göre (28 Mayıs MÖ 585’te gerçekleştiği kabul edilen) Güneş tutulmasını önceden hesaplayıp haber vermiştir. Astronomi ile uğraşan ve gün dönümlerini önceden hesaplayan biri olarak astronomdur. Gölgemizin bizimle aynı uzunlukta olduğu zamanı gözleyerek, piramitleri gölgelerine bakarak ölçmüştür. Aynı zamanda Nil nehrinin yükselmesinin rüzgara bağlı olduğunu bulmuştur. (Etesios rüzgarları nehrin tersine eserek onun denize dökülmesini engelliyorlarmış ve sular da taşıyormuş.)
Matematik-geometri
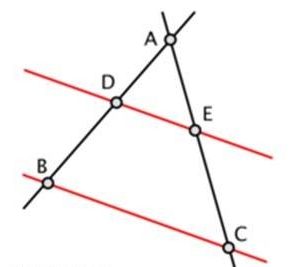
Thales Teoremi : 
Matematik alanında çığırlar açmış birisidir. Eski Yunan bilginlerinden Kallimakhos’un aktardığı bir düşünceye göre denizcilere kuzey takım yıldızlarından Büyükayı yerine Küçükayı’ya bakarak yön bulmalarını öğütlemiştir. Aynı zamanda Mısırlılardan geometriyi öğrenip Yunanlara tanıtmıştır. Bulduğu bazı geometri teoremleri şunlardır:
- Çap çemberi iki eşit parçaya böler.
- Bir ikizkenar üçgenin taban açıları birbirine eşittir.
- Birbirini kesen iki doğrunun oluşturduğu ters açılar birbirine eşittir.
- Köşesi çember üzerinde olan ve çapı gören açı, dik açıdır.
- Tabanı ve buna komşu iki açısı verilen üçgen çizilebilir.
- Genelleştirilmiş 1959 Thales teoremine göre, E noktası AC doğru çizgisi üzerinde olmasa,içerde veya dışarda olsa bile CB/BA=(AB^t-BD^t)^(1/t)/ED vardır. (t=1) hali bilinen klasik Thales teoremidir.
Pisagor
Pisagor ya da Pythagoras (Yunanca: Πυθαγόρας), MÖ 570 – MÖ 495 yılları arasında yaşamış olan İyonyalı filozof. Matematikçi vePisagorculuk olarak bilinen akımın kurucusudur.
En iyi bilinen önermesi, kendi adıyla anılan Pisagor önermesidir. “Sayıların babası” olarak bilinir. Pisagor ve öğrencileri her şeyin matematikle ilgili olduğuna, sayıların nihai gerçek olduğuna, matematik aracılığıyla her şeyin tahmin edilebileceğine ve ölçülebileceğine inanmışlardır.
Kendisini filozof (Yunanca:φιλοσοφος), yani bilgeliğin dostu olarak adlandıran ilk kişiydi. Pisagor, düşüncelerini yazıya dökmediği için onun hakkında bildiklerimiz öğrencilerinin yazılarında anlattıklarıyla sınırlıdır. Pisagor’a atfedilen birçok eser gerçekte onun öğrencilerinin olabilir.
Bir dik açılı üçgende dik kenarların her birinin uzunluklarının karelerinin toplamları, hipotenüsün uzunluğunun karesine eşittir. Bu teoremin matematik formülle ifadesi şöyledir: c² = a²+ b²
Pisagor’un bilim ve sanata katkıları
- Matematik ve astronomiye katkıları olmuştur.
- Ürettiği bağıntıya Pisagor bağıntısı adını vermiştir.
- Pisagor, teoremi ile irrasyonel sayıları buldu.
- Müziğin matematiksel oranlara indirgenebileceğini ortaya koymuş ve diatonik skalayı keşfetmiştir.
- Günümüzde bazı bilim adamlarının çok sıcak baktığı “kürelerin müziği” adıyla bilinen “kürelerin armonisi” önermesini ortaya atmıştır.
- Müzikle tedavi çalışmalarıyla tıbba katkıda bulunmuştur.
- Bir iddiaya göre, Dünya’nın yuvarlak olduğunu ve ikili bir hareket içinde olduğunu biliyordu ve bunları yalnızca inisiyelerine açıklamıştı ki, bu açıklamaları, ezoterik doktrin yoluyla kuşaktan kuşağa aktarılarak bu bilgilerin kabulünde rol oynamıştır.
- (3,4,5) ve (5,12,13) özel üçgenlerini bulmuştur
- Çarpım tablosunu ilk olarak o kullandı.
Elealı Zenon
Elealı Zenon veya Zeno, Parmenides’in izleyicisi olan Antik Yunan filozofu. Elea Okulu’nun en önemli filozofları arasında yer alır.
Zeno, hocası Parmenides’in Bir’ci anlayışını ve yalnızca Varlık’ın değişmez gerçek olduğunu öne süren görüşünü geliştirmiş, çokluk ve değişmenin gerçek olduğunu savunan karşıt görüşlerin tezlerine karşı mantıksal güçlükleri gözler önüne seren dolaylı kanıtlarla değişimin olanaksızlığını göstermeye çalışmış, ileri sürdüğü örneklemeleriyle felsefe tarihinde ün kazanmıştır. MÖ 490 – MÖ 430 yılları arasında yaşadığı rivâyet edilse de doğum ve ölüm tarihi kesin değildir.
Zeno bir mantık ustası ve diyalektik düşüncenin en önemli geliştiricilerinden biridir. İleri sürdüğü önermeler, felsefe tarihinin en önemli paradoksları arasında yer almaktadır. Bunlardan en ünlüleri Aşil paradoksu ve Ok paradoksu olarak belirtilebilir. Zeno bu örneklemelerden hareketle değişimi bir yanılsama olarak formüle eden felsefesini temellendirir.
İlk paradoksta, ünlü bir Yunan koşucu olan Aşil, bir kaplumbağayla yarışacaktır. Kaplumbağa biraz daha önde olacaktır koşuya başlarken. Zeno, bu koşuda hızlı Aşil’in hiçbir zaman kaplumbağayı geçemeyeceği, bunun mantıksal olarak mümkün olmadığını öne sürer. Çünkü her seferinde Aşil’in aşması gereken bir mesafe kalacaktır, kaplumbağanın bulunduğu noktaya her gelişinde kaplumbağa bir başka noktaya geçmiş olacaktır ve Aşil’in onu geçebilmesi için her seferinde bu noktaları öncelikle geçmiş olması gerekir. Ok paradoksunda da benzer bir sonuca varılır.
Buradaki temel argüman şöyledir: Mesafe sonsuz noktalardan oluşmaktadır ve bunlar sonlu bir süre içinde geçilemezdir. Böylece Zeno mantıksal ve diyalektik olarak bilinen diyalektikcilerin tam karşıt yönünde hareketin ve değişmenin olanaksız olduğunu, bunların bir yanılsama olduğunu ve temelde varlık’ın değişmeyen bir halinde bulunduğunu öne sürer.
Öklid
Öklid (Yunanca: Εὐκλείδης — Eukleídēs) MÖ 330 – 275 yılları arasında yaşamış İskenderiyeli bir matematikçidir.
Öklid gelmiş geçmiş matematikçilerin içinde adı geometri ile en çok özdeşleştirilen kişidir. Geometri dünyasında kapladığı bu seçkin yeri kendisinin büyük bir matematikçi olmasından çok, geometrinin başlangıcından kendi zamanına kadar bilinen ismi ile Öğeler adını taşıyan kitabında toplamıştır. Öklid derlemesinin tutarlı bir bütün olmasını sağlamak için, kanıt gerektirmeyen apaçık gerçekler olarak 5 aksiyom ortaya koyar. Diğer bütün önermeleri bu aksiyomlardan çıkarır.
Eğitimini Akademi’de tamamladıktan sonra İskenderiye’de büyük bir matematik okulu kuran Öklid, çağlar boyu matematikle ilgilenen hemen herkesin gözdesi olmuştur. Geometriyi ispat ve aksiyomlara dayalı bir dizge olarak işleyen 13 ciltlik kitabı “Elementler” bu alandaki ilk kapsamlı çalışmaydı. Kendinden önceki Tales, Pisagor, Platon, Aristoteles gibi matematikçi ve geometricilerin çalışmalarını temel alan Öklid’in bu yapıtı, iki bin yıl boyunca önemli bir başvuru kaynağı olarak kullanılmıştır. Düzlem geometrisi, aritmetik, sayılar kuramı, irrasyonel sayılar ve katı cisimler geometrisi Öklid’in kitabında ele aldığı başlıca konulardı. Öklid’in her önermeyi daha önceki önermelerden çıkarma yöntemi, kendisine atfedilen “geometrinin babası” sözünü de haklı kılar. Kitapta yer alan aksiyomlara, teoremlere ve ispatlara dayanan sentez yöntemlerinin Batı düşüncesi üzerindeki etkisinin Kitabı Mukaddes’ten sonra ikinci sırada yer aldığı söylenir. Russell, Öğeler’in bugüne kadar yazılmış en büyük kitap olduğunu ileri sürer. Einstein ise “Gençliğinde bu kitabın büyüsüne kapılmamış bir kimse, kuramsal bilimde önemli bir atılım yapabileceği hayaline kapılmasın” der.
Öklid geometrisi 19. yüzyılın başına kadar rakipsiz kaldı. Hatta 20. yüzyılın ortalarına kadar bile orta öğretimde geometri, Öklid’in öğelerine bağlı olarak okutuldu.
Öklid’in yaşamı konusunda hemen,hemen hiçbir şey bilinmiyor. Önceleri bir Yunan kenti olan Megara’da doğduğu sanıldıysa da, sonradan Megaralı Öklid’in, Öğeler’in yazarı İskenderiyeli Öklid’den yüzyıl kadar önce yaşamış olan bir felsefeci olduğu ortaya çıkmıştır.
Öklid üzerinde çalıştığı proje hakkında diyor ki: “bir doğru istenildiği kadar uzatabilir.” ve “İki noktadan bir ve yalnız bir doğru geçer.”
Öklid’in aksiyomları
İngilizcede postula ve aksiyom kelimeleri aynı anlama gelebilmektedir. O yüzden bazı kaynaklarda geçen postula ve aksiyom adı altında verilen farklı tanımlamalarda sorunlar vardır. Birçok Türkçe eserde karşılaşılabilen bir sorundur bu. İngilizce vikipedi de [1] postula ve aksiyom şeklinde iki ayrı şeyden bahsedilmemektedir. Bunun yerine postulalardan (aksiyomlardan) ve buna ek olarak ortak kanılardan (common notions) bahsedilmektedir.
Öklid’in postulaları veya aksiyomları:
- Herhangi bir noktadan herhangi başka bir noktaya bir düz doğru çizmek mümkündür.
- Bir tane doğru parçasını her iki yöne de sürekli bir şekilde uzatmak mümkündür.
- Herhangi bir merkez ve herhangi bir yarıçap ile bir çember tanımlamak mümkündür.
- Bütün dik açıların birbirine eşit olduğu doğrudur.
- Eğer iki doğru ile kesişen en bir doğru çizilirse, iki doğrunun birbirine bakan tarafında yer alan ve onları kesen doğrunun bir tarafında kalan iki açının toplamı iki dik açıdan küçükse bu iki doğru açıların toplamının iki dik açıdan az olduğu tarafta uzatılmaya devam ederlerse ilerde bir noktada kesişecekleri doğrudur. (Bu postula paralel doğrular kesişmez şeklinde bilinen postuladır.)
Ortak kanılar:
- Bir şeye eşit olan başka şeyler birbirlerine de eşittirler.
- Eğer eşit miktarlara eşit miktarlar eklenirse, elde edilen bütünler de birbirlerine eşittir.
- Eğer eşit miktalardan eşit miktarlar çıkarılırsa, kalanlar da birbirlerine eşittir.
- Birbirleriyle çakışan (özelikleri açısandan örtüşen) şeyler birbirlerine eşittir.
- Bütün parçadan büyüktür.
Arşimet
Arşimet (Antik Yunanca: Ἀρχιμήδης (y. MÖ 287, Siracusa – y. MÖ 212 Siracusa), Yunan[kaynak belirtilmeli] matematikçi, fizikçi, astronom,filozof ve mühendis.
Antik dünyanın ilk ve en büyük bilim adamı olarak kabul edilir. Hidrostatiğin ve mekaniğin temelini atmıştır.
Bir hamamda yıkanırken bulduğu iddia edilen suyun kaldırma kuvveti bilime en çok bilinen katkısıdır. Bu kuvvet cismin batan hacmi, içinde bulunduğu sıvının yoğunluğu ve yerçekimi ivmesinin çarpımına eşittir. Ayrıca, pek çok matematik tarihçisine göre integral hesabın kaynağı da Arşimet’tir.
Arşimet Buluşları
Mekanik
Arşimet’in mekanik alanında yapmış olduğu buluşlar arasında bileşik makaralar, sonsuz vidalar, hidrolik vidalar ve yakan aynalar sayılabilir. Bunlara ilişkin eserler verilmemiş, ancak matematiğin geometri alanına, fiziğin statik ve hidrostatik alanlarına önemli katkılarda bulunan pek çok eser bırakmıştır.
İlk defa denge prensiplerini ortaya koyan bilim adamı da Arşimet’tir. Bu prensiplerden bazıları şunlardır:
- Eşit kollara asılmış eşit ağırlıklar dengede kalır.
- Eşit olmayan ağırlıklar eşit olmayan kollarda aşağıdaki koşul sağlandığında dengede kalırlar: f1 • a = f2 • b
Bu çalışmalarına dayanarak söylediği “Bana bir dayanak noktası verin Dünya’yı yerinden oynatayım.” sözü yüzyıllardan beri dillerden düşmemiştir.
Geometri
Geometriye yapmış olduğu en önemli katkılardan birisi, bir kürenin yüzölçümünün 4 r2 ve hacminin ise 4/3
r2 ve hacminin ise 4/3  r3 eşit olduğunu kanıtlamasıdır. Bir dairenin alanının, tabanı bu dairenin çevresine ve yüksekliği ise yarıçapına eşit bir üçgenin alanına eşit olduğunu kanıtlayarak pi değerinin 3 +l/7 ve 3 +10/71 arasında bulunduğunu göstermiştir. Başka bir değişle bu formülleri suyun hacim kullanma esnasında alabileceği özkütle çapıdır.
r3 eşit olduğunu kanıtlamasıdır. Bir dairenin alanının, tabanı bu dairenin çevresine ve yüksekliği ise yarıçapına eşit bir üçgenin alanına eşit olduğunu kanıtlayarak pi değerinin 3 +l/7 ve 3 +10/71 arasında bulunduğunu göstermiştir. Başka bir değişle bu formülleri suyun hacim kullanma esnasında alabileceği özkütle çapıdır.
Matematik
Arşimet’in en parlak matematik başarılarından biri de, eğri yüzeylerin alanlarını bulmak için bazı yöntemler geliştirmesidir. Bir parabol kesmesini dörtgenleştirirken sonsuz küçükler hesabına yaklaşmıştır. Sonsuz küçükler hesabı, bir alana tasavvur edilebilecek en küçük parçadan daha da küçük bir parçayı matematiksel olarak ekleyebilmektir. Bu hesabın çok büyük bir tarihi değeri vardır. Sonradan modern matematiğin gelişmesinin temelini oluşturmuş, Newton ve Leibniz’in bulduğu diferansiyel denklemler ve integral hesap için iyi bir temel oluşturmuştur. Arşimet, Parabolün Dörtgenleştirilmesi adlı kitabında, tüketme metodu ile bir parabol kesmesinin alanının, aynı tabana ve yüksekliğe sahip bir üçgenin alanının 4/3’üne eşit olduğunu ispatlamıştır.
Hidrostatik
Arşimet, kendi adıyla tanınan “sıvıların dengesi kanununu” da bulmuştur. suya batırılan bir cismin taşırdığı suyun ağırlığı kadar kendi ağırlığından kaybettiğini fark ederek hamamdan “eureka” (buldum, buldum) diye haykırarak çırıl çıplak dışarı fırlaması, onunla ilgili en çok bilinen bir hikayedir. Söylendiğine göre, bir gün Kral II Hieron yaptırmış olduğu altın tacın içine kuyumcunun gümüş karıştırdığından kuşkulanmış ve bu sorunun çözümünü Arşimet’e havale etmiştir. Bir hayli düşünmüş olmasına rağmen sorunu bir türlü çözemeyen Arşimet, yıkanmak için bir hamama gittiğinde, hamam havuzunun içindeyken ağırlığının azaldığını hissetmiş ve “evreka, evreka” diyerek hamamdan fırlamıştır. Arşimet’in bulduğu şey; su içine daldırılan bir cismin taşırdığı suyun ağırlığı kadar ağırlığını kaybetmesi ve taç için verilen altının taşırdığı su ile tacın taşırdığı su mukayese edilerek sorunun çözülebilmesi idi. Çünkü her maddenin özgül ağırlığı farklı olduğundan aynı ağırlıktaki farklı cisimler farklı hacme sahiptir. Bu nedenle suya batırılan aynı ağırlıktaki iki farklı cisim farklı miktarlarda su taşırırlar.
Pergeli Apollonius
Pergeli Apollonius (d. MÖ 262 Perge – ö. MÖ 190, İskenderiye), Yunan matematikçi.
Zamanında çok bilinmeyen, fakat 1600 yıllarında değeri anlaşılan Yunan matematikçilerinden biri Pergeli Apollonius’tur. Eski devirlerin en büyük matematikçilerinden biridir. MÖ 267 veya 262 yıllarında, Pamfiye denilen Teke sancağının Perge kentinde dünyaya gelmiştir. Mısır’ın İskenderiye kentine giderek, Öklid’ten sonra gelen matematikçilerden dersler alarak kendini yetiştirmiştir. Bir aralık Bergama’ya giderek orada kalmış, burada matematikçi Ödemus ve eski Bergama hükümdarı Atal ile ilmi ilişkilerde bulunmuştur. Matematikçi Pappus, Apollonius’un, bencil, üne düşkün, kibirli ve gururlu birisi olduğunu yazmaktadır. Apollonius’un yaptığı çalışmalar ve buluşları onun bu zayıf taraflarını örtecek kadar kuvvetlidir. Çarpmaya ait birçok buluşu vardır. Tümü geometriye ait olan yedi sekiz kitabı vardır. Koniklere ait buluşları onu şöhretin zirvesine çıkarmıştır. Birçok eserinin kaybolmasına karşın, bazı yapıtları Pappus tarafından yeniden ortaya çıkarılmıştır.
Öklid geometrisini benimseyerek onu daha ileri düzeylere götürmüştür. Teorik ve sentetik geometrici olarak, 19. yüzyıldaki Steiner’e kadar Apollonius’un bir eşine daha rastlanamaz. Konikler adı altında bugün bildiğimiz elips, çember, hiperbol ve parabol kesişimlerine ait problemlerin birçoğu Apollonius tarafından bulunmuştur. Konikler her ne kadar Apollonius’tan 150 yıl kadar önce üzerinde çalışılmışsa da, Apollonius kendisinden önceki çalışmaları ve kendi öz buluşlarını sekiz kitapta toplamıştır. Bunların çoğu onun çalışmaları ile ilerlemiştir. Yedi tane de yeni araştırması vardır. Bu araştırmaların bazıları Arapça’dan çevirmedir. Yine, analitik geometri özelliklerinin hemen hemen tümünü Apollonius’a borçluyuz.
Dairesel tabanlı ve tepesinin her iki tarafından sonsuza kadar uzatılmış bir koni bir düzlemle kesilirse, düzlemle koni yüzeyinin kesişimi olan eğri, doğru, çember, hiperbol, elips veya parabol olacağını ilk kez Apollonius göstermiştir. Merminin yörünge denkleminin bir parabol olacağı yine Apollonius tarafından bulunmuştur. Ayrıca, astronomide önemli buluşları vardır.
Elips, hiperbol ve parabol, Eflatun tarafından mekanik eğriler olarak adlandırılmıştır. Bu eğriler, yalnız cetvel ve pergel yardımıyla çizilemezler. Buna karşın, pergel ve cetvel yardımıyla, bu eğrilerin istenilen sayıda noktalarını elde edebiliriz. Apollonius ve konikler üzerine çalışma yapanların diğer bir hizmeti de, Kepler ve Kopernik’in Güneş ve gezegenlerin yörüngelerini hesaplamasında kullanmasıdır. Eğer bu geometriciler olmasaydı, Newton çekim kanununu belki de hiç bulamayacaktı. Yani, Kepler’in gezegenlerin yörüngeleri hakkındaki ince ve ustalıklı kullandığı hesaplamaları, Newton’un çekim kanununa ortam hazırlamıştır. Pergel ve cetvel yardımıyla üç çembere teğet çizme, Apollonius problemi olarak bilinir. Yine, sabit iki noktaya olan uzaklıkları oranı sabit olan noktaların geometrik yeri, bu sabit noktaları birleştiren doğru parçasını, verilen orana göre içten ve dıştan bölen noktalar arasındaki uzaklığı çap kabul eden bir çemberdir.
Hipparkos
Hipparkos (Yunanca: Ἵππαρχος, Hipparkhos; MÖ 190 – MÖ 120), Helenistik dönemde yaşamış Eski Yunan gökbilimci, matematikçi vecoğrafyacı. Trigonometrinin kurucusu olarak tanınmaktadır.
Anadolu’daki Nikea (bugünkü İznik) kentinde doğdu. Yaşamının büyük bölümünü Rodos’ta geçiren ve orada ölen Hipparkos, daha çokyıldızlara ilişkin gözlemleriyle tanındı. Çıplak gözle görülebilen yıldızları parlaklıklarına göre sınıflandırdı. Ayın ve Güneş’in uzaklıklarını bulmaya yönelik çalışmalar da yapan Hipparkos, matematiğin bir dalı olan trigonometriyi bulmasının yanında yeryüzündeki her noktanın yerinienlem-boylam dereceleriyle belirtme yöntemini ilk uygulayan kişi oldu.
Menelaus
İskenderiyeli Menelaus’a izafe edilen Menelaus teoremi düzlemsel geometride üçgenler üzerine bir teoremdir. A, B ve C noktalarından oluşan ABC üçgeninde BC, AC ve AB doğruları üzerinde bulunan ve üçgenin köşelerinden ayrık D, E ve F noktalarının aynı doğru üzerinde olabilmesi ancak ve ancak:
denkleminin sağlanması ile mümkündür.
Bu denklemde, örneğin  , eksi değer alabilen doğru parçalarını simgeler. Örnek olarak
, eksi değer alabilen doğru parçalarını simgeler. Örnek olarak  kesiri sadece DEF doğrusu AB kenarını kestiğinde artı değer alabilecek şekilde tanımlanmalıdır, çünkü sadece bu durumda iki doğru parçası aynı yönde ölçülmektedir ve bu durum diğer kesirler için de geçerlidir. Matematikçiler arasında bu teoremin yanlış olduğu üzerine süregelen bir şaka vardır (bunun yerine Ceva teoremi nin kullanılması gerektiği söylenir).
kesiri sadece DEF doğrusu AB kenarını kestiğinde artı değer alabilecek şekilde tanımlanmalıdır, çünkü sadece bu durumda iki doğru parçası aynı yönde ölçülmektedir ve bu durum diğer kesirler için de geçerlidir. Matematikçiler arasında bu teoremin yanlış olduğu üzerine süregelen bir şaka vardır (bunun yerine Ceva teoremi nin kullanılması gerektiği söylenir).
İskenderiyeli Heron
Heron (d. MS 10-ö. MS 70), Antik Çağ’da yaşamış Yunan matematikçi ve mühendistir. Roma zamanında Mısır’ın İskenderiye kentinde yaşamıştır. Antik çağın en büyük deneycilerinden biri olarak kabul edilen Heron, çalışmalarıyla Hellenistik geleneksel bilimin öncüsü olmuştur. Kitaplarının en az 13 tanesinin günümüze ulaştığı biliniyor.
Heron buhar gücüyle çalışan Aeolipile adında bir cihazın mucidi olarak tanınır ancak, karada rüzgar enerjisinin en erken örneğini teşkil eden Yel Değirmeni’nin mucididir. Bazı fikirleri “Ctesibius”tan esinlenmiştir.
İcataları
Heron’un otomatlar yani gizemli araçlar konusundaki ilk çalışması sihirli sürahidir. Sürahinin sapında bir delik vardır; sürahideki suyu boşaltmaya çalışan kişi, eğer bu deliği parmağıyla kaparsa su akmaz, açarsa tekrar akar. Gösterilerde suyun bazen akması bazen akmaması seyircilere hayli eğlenceli geldiğinden, Heron da okulun diğer temsilcileri gibi bu buluşunu daha çok eğlence amaçlı kullanmıştı. Düzeneğin esasını hava ve boşluk hakkındaki bilgiler oluşturuyordu. Heron Pneumatica (Pnömatik-Hava Basıncı) adlı kitabında çok sayıda benzer düzenek tarif etmişti. Heron hava, hava basıncı ve boşluk konusunda yaptığı çalışmalarla “aeolipile” adı verilen ilk buhar türbinini de icat etmişti. Son derece basit hazırlanmış düzenek, içi su ile dolu bir hazne ve üzerinde iki delik bulunan metal bir küreden oluşur. Metal küre su haznesinin üzerine iki boruyla sabitlenmiştir. Haznenin altında ateş yakıldığında, bir süre sonra su kaynayıp buharlaşan su iki boru aracılığıyla metal küreye dolar. Küreye dolan buhar, üzerindeki iki köşeli borudan basınçlı bir şekilde dışarıya çıkar, çıkarken de oluşturduğu kuvvetin etkisiyle küre kendi etrafında döner. Buhar arttıkça gittikçe daha hızlı dönen metal küre, etrafa basınçlı su buharı püskürtmeye başlar, basınçtan dolayı dönen küre aynı zamanda kuvvetli bir ıslık sesi çıkarır. Metal kürenin dönme hızı ateşin gücüne bağlıdır. Çünkü ateş ne denli güçlü olursa, su da o kadar hızlı buharlaşacak, kürenin dönüşü de o kadar hızlı olacaktır. Metal kürenin ses çıkararak dönmesi insanları heyecanlandırdığından, o gün için harika bir oyuncak olarak görülen bu basit araç, aslında bilimsel bir ilkenin, Isaac Newton’un “her etki kendine eşit ve zıt bir karşı etki yaratır” şeklinde ifade edilen üçüncü hareket yasasının uygulanışı olması bakımından dikkat çekicidir. Buhar türbinin temelini oluşturacak bir düşüncenin ürünüolan bu aracı da Heron gösteri amacıyla kullanmıştır.
Heron’un hava basıncı, boşluk ve denge ilkelerinden yararlanarak yaptığı çeşitli araçlardan biri de bir tapınak kapısının otomatik olarak açılıp kapanmasını sağlayan düzenekti. O dönemde her tapınağın yanında bir sunak taşıvardı. Heron’un yaptığı düzenek sayesinde, bu sunaktaşının üzerinde bir ateş yakılınca tapınağın kapısı kendiliğinden açılıyor, ateş sönünce de kapanıyordu. Düzenek şöyleydi: Sunak taşının (A) altındaki boru su dolu bir kabın (B) içine giriyor. B kabının içinden çıkan diğer bir boru da (C), içinde su bulunan ve L ağırlığıyla dengelenmiş D kabına bağlanıyor. D kabı aynı zamanda kapı kanatlarının açılıp kapanmasını sağlayan sütunlara bağlı. D kabını dengede tutan L ağırlığı da iple sütunlara bağlı. Düzenek denge durumundayken kapı kapalı konumdadır. Heron bu kapının kendiliğinden açılıp kapanmasını sağlıyor. Düzenek şöyle çalışıyor: Ateş yakıldığında sunak taşının (A) içindeki hava ısınarak genişler ve B küresinin içindeki suya basınç yapar. Bu basınç nedeniyle, suyun bir kısmı C aracılığı ile D kovasına geçer. İlk konumda, yani kapı kanatlarının kapalı olduğu konumda L ağırlığı ile dengede olan kova, suyun bir kısmının içine akmasıyla ağırlaşır, sütunlar üzerine sarılmış ipi çeker, kapı kanatlarına bağlı olan sütunları döndürür ve kapı açılır. Ateş söndüğünde ise hava basıncı azalır, daha önce kovaya geçen su geri döner, kova hafifler, L ağırlığı ile dengeye gelir, bu kez sütunlar aksi yöne dönerek kapı kanatlarını kapatır.
Batlamyus
Klaudyos Batlamyus (Antik Yunanca: Κλαύδιος Πτολεμαίος, Klaudyos Ptolemaios), İskenderiye’li Yunanı matematikçi, coğrafyacı veastronom. Yaklaşık olarak 85 ve 165 yılları arasında yaşadığı kabul edilir.
Geç İskenderiye Dönemi’nde yaşamış (MS 2. yüzyılın ilk yarısı) ünlü bilim adamlarındandır. Hayatı hakkında hemen hemen hiçbir bilgi bulunmamaktadır. Müslüman astronomlar 78 yaşına kadar yaşadığını söylemektedir. Yunan asıllı bir Mısırlı, veya Mısır asıllı bir Yunan olduğu iddia edilmektedir.
Batlamyus astronomi, matematik, coğrafya ve optik alanlarına katkılar yapmıştır; ancak en çok astronomi çalışmalarıyla tanınır. Zamanına kadar ulaşan astronomi bilgisinin sentezini yapmış ve bunları Mathematike Syntaxis (Matematik Sentezi) adlı yapıtında toplamıştır. Bu eser daha sonra Megale Syntaxis (Büyük Derleme) olarak anılmış ve Arapça’ya çevrilirken başına Arapça’dakiler harf-i tarif takısı olan el getirildiği için, ismi el-mecistî biçimine dönüşmüştür; daha sonra Arapça’dan Latince’ye çevrilirken Almagest olarak adlandırıldığından, bugün Batı dünyasında bu eser Almagest adıyla tanınmaktadır.
Optik araştırmaları
Aynı zamanda döneminin önde gelen optik araştırmacılarından olan Batlamyus, daha önceki optikçilerin çoğu gibi, görmenin gözden çıkan görsel ışınlar yoluyla oluştuğu görüşünü benimsemiştir. Ancak, görsel yayılımın fiziksel yorumunu da vermiş ve bu yayılımın, kesikli ve aralıklı koni biçiminde değil de, kesiksiz ve sürekliliği olan piramit biçiminde olduğunu belirtmiştir. Şayet böyle olmasaydı, yani ışınlar gözden sürekli olarak çıkmasaydı, nesneler bütün olarak görülemezlerdi. Buna rağmen, Batlamyus’un görsel piramit fikri, optikçiler arasında rağbet görmemiş ve görme söz konusu olduğunda daha çok koni biçimi göz önüne alınmıştır. Daha sonra da İslâm dünyasında bilginlerin görsel koni fikrine dayandıkları ve görme geometrisini bunun üzerine kurdukları görülmektedir.
Batlamyus, katoptrik (yansıma) konusuyla da ilgilenmiş ve ayrıntılı deneyler sonucunda üç prensip ileri sürmüştür:
- Aynada görünen nesne, gözün konumuna bağlı olarak aynadan nesneye yansıyan görsel ışın yönünde görünür.
- Aynadaki görüntü, nesneden ayna yüzeyine çizilen dikme yönünde ortaya çıkar.
- Geliş ve yansıma açıları eşittir.
Bu üç prensipten ilk ikisini kuramsal, üçüncüsünü ise deneysel olarak kanıtlayan Batlamyus, ayna yüzeyine gelen ışının eşit açıyla yansıdığını gösterebilmek için, derecelenmiş ve tabanına ayna yerleştirilmiş olan bakır bir levha kullanmıştır. Bir ışın hüzmesini levhaya teğet biçimde ayna yüzeyine gönderip, gelme ve yansıma açılarının büyüklüklerini belirlemiş ve bunların eşit olduğunu görmüştür. Batlamyus bu deneyini küresel ve parabolik bütün aynalar için tekrarlayarak, sonucun doğruluğunu kanıtlamıştır.
Batlamyus, dioptrik (kırılma) konusuyla da ilgilenmiş ve ışığın bir ortamdan diğerine geçerken yoğunluk farkından dolayı yön değiştirmesinin nedenini araştırmıştır. Bu araştırmanın sonucunda, az yoğun ortamdan çok yoğun ortama geçen ışının, normale yaklaşarak ve çok yoğun ortamdan az yoğun ortama geçen ışının ise normalden uzaklaşarak kırıldığını ve kırılma miktarının yoğunluk farkına bağlı olduğunu ileri sürmüştür.
Konuyu ele alırken benimsediği bazı prensiplerde bunu açıkça görmek olanaklıdır:
- Görsel ışın az yoğundan çok yoğuna veya çok yoğundan az yoğuna geçtiğinde kırılır.
- Görsel ışın doğrusal olarak yayılır ve farklı yoğunluktaki iki ortamı birbirinden ayıran sınırda yön değiştirir.
- Gelme ve kırılma açıları eşit değildir, fakat aralarında niceliksel bir ilişki vardır.
- Görüntü, gözden çıkan ışının devamında ortaya çıkar.
Batlamyus ortam farklılıklarından dolayı ışığın uğradığı değişimleri, aynı zamanda kırılma kanununu da içerecek şekilde deneysel olarak göstermeye çalışmış ve çeşitli ortamlardaki (havadan cama, havadan suya ve sudan cama) kırılma derecelerini gösteren cetveller hazırlamıştır. Ancak verdiği değerler küçük açılar dışında tutarlı olmadığı için kırılma kanununu elde edememiştir.
Astrolojik çalışmaları
Batlamyus, daha önce Babil ve Yunan astronomları ve astrologları tarafından derlenmiş bilgi birikiminden yararlanarak astrolojiyi de sistematize etmiştir. Dört bölümden oluştuğu içinTetrabiblos (Dört Kitap) olarak adlandırdığı yapıtında, gezegenlerin nitelik ve etkileri, burçların özellikleri, uğurlu ve uğursuz günlerin belirlenmesi gibi astroloji kapsamındaki konular hakkında ayrıntılı bilgiler vermiştir. Ortaçağ ve Yeniçağ astrolojisi bu kitabın sunmuş olduğu birikime dayanacaktır.
Astroloji bir bilim değildir, ama astronomi ile birlikte doğmuş ve yaklaşık olarak 18. yüzyıl’a kadar bu bilimin gelişimini, kısmen olumlu kısmen de olumsuz yönde etkilemiştir; bu nedenle astronomi tarihi araştırmalarında astrolojiye ilişkin gelişmelerden de bahsetmek gerekir.
Coğrafya araştırmaları
Batlamyus, coğrafya araştırmalarına da öncülük etmiş ve Coğrafya adlı yapıtıyla matematiksel coğrafya alanını kurmuştur. Bu kitap Kristof Kolomb’a kadar bütün coğrafyacılar tarafından başvuru kitabı olarak kullanılmıştır.
Almagest’ten sonra yazılan Coğrafya, sekiz kitaba bölünmüştür ve matematiksel coğrafya ile haritaların çizilebilmesi için gerekli bilgilere tahsis edilmiştir; Almagest gibi Coğrafya da derleme bir eserdir; Batlamyus bu kitabı hazırlarken Eratosthenes, Hiparkhos, Strabon ve özellikle de Surlu Marinos’tan büyük ölçüde yararlanmıştır.
Coğrafya’nın Birinci Kitabı, Dünya’nın -ya da doğrusunu söylemek gerekirse Yunanlar tarafından bilinen Dünya’nın- büyüklüğü vekartografik izdüşüm yöntemleri hakkında ayrıntılı bilgiler verir.
İkinci Kitap’la Yedinci Kitap arasında, tanınmış memleketlerdeki önemli yerlerin, yani önemli kentlerin, dağların ve nehirlerin enlem ve boylamları verilerek Dünya’nın düzenli bir tasviri yapılır. Enlem ve boylamlardan, yani bir başlangıç dairesine olan uzaklıklardan söz eden ilk bilgin olan Batlamyus’un enlem ve boylam tablolarıyla betimlemeye çalıştığı Dünya, kabaca 20° güneyden, 65° kuzeye; batıdaki Kanarya Adaları’ndan, bunların yaklaşık olarak 180° doğusundaki bölgelere kadar uzanmaktadır. Bunun dışında kalan bölgeler ise Yunanlar ve dolayısıyla Batlamyus tarafından tanınmamaktadır. Söz konusu tablolar, haritaların çizilmesini olanaklı kılmaktadır ve belki de bu haritalar eserin eski nüshalarında mevcuttur. Astronomi bilgilerini kapsayan Sekizinci Kitap’ta bunlara atıflar yapılmıştır.
Ancak Batlamyus’un coğrafya anlayışı yeterince geniş değildir. İklim, doğal ürünler ve fiziki coğrafyaya giren konularla hiç ilgilenmemiştir. Başlangıç meridyenini sağlam bir şekilde belirleyemediği için, vermiş olduğu koordinatlar hatalıdır. Ayrıca, Yer’in büyüklüğü hakkındaki tahmini de doğru değildir. Ancak Kristof Kolomb bu yanlış tahminden cesaret alarak Batı’ya doğru gitmiş veKuzey Amerika’ya ulaşmıştır.

